快速排序 Quick Sort

快速排序是一种高效的排序方法，于 1963 年由 Tony Hoare 发布。

原理

快速排序是一种分治（Divide-and-Conquer）算法。它的主要思路是：

• 从数组中挑选一个元素作为基准元素（Pivot）
• 分区（Partition）:将数组中小于或等于基准元素的值移动到基准元素前面，将大于基准元素的值移动到基准元素后面。每次分区操作，都会将该基准元素放置于其该在的位置。
• 递归对左边和右边的子序列进行快速排序

图示

可以通过动画演示理解, 以下网上找的两个动画。如果你想操作不同的参数来演示，可以上这个网站visualgo.net动手试试。

图示1

图示2

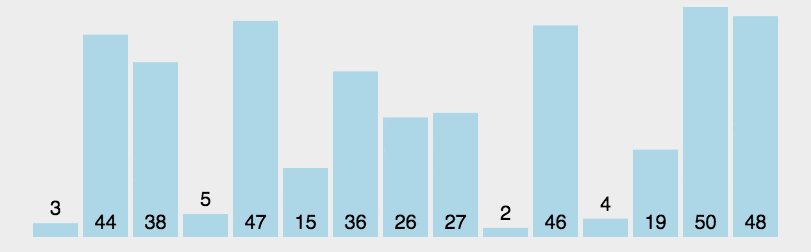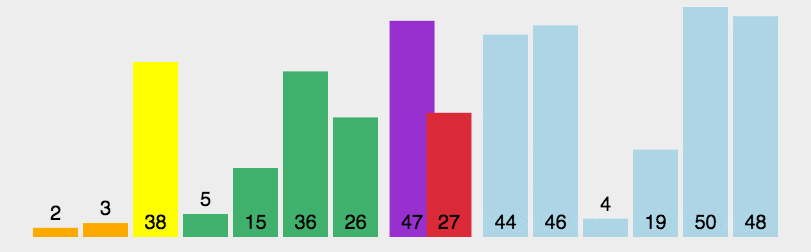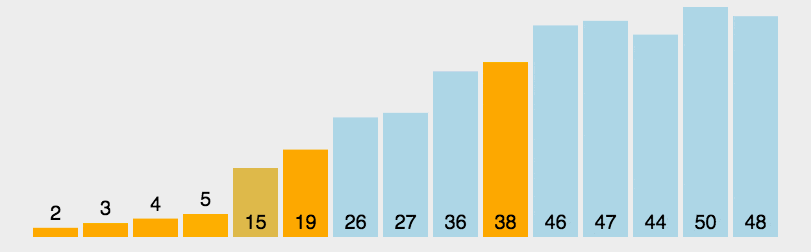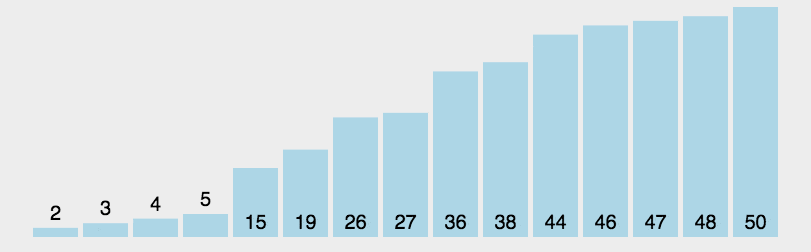
代码实现

Lomuto 分区算法

利用快慢指针，找到最终 pivot 的位置。

const partition = (arr, low, high) => {
  const pivot = arr[high]
  let pIndex = low;
  for (let i = low; i < high; i++) {
    if (arr[i] < pivot) {
      [arr[i], arr[pIndex]] = [arr[pIndex], arr[i]]
      pIndex++
    }
  }
  [arr[pIndex], arr[high]] = [arr[high], arr[pIndex]]
  return pIndex
}
const quickSort = (arr, low = 0, high = arr.length - 1) => {
  if (low >= high) {
    return
  }

  const pivotIndex = partition(arr, low, high)
  quickSort(arr, low, pivotIndex - 1)
  quickSort(arr, pivotIndex + 1, high)
}

Hoare 分区算法

Hoare 分区算法比 Lomoto 分区算法少了将近三倍的数据交换。

• 使用两个指针 left, right。起始 left 指向第一个元素，right 指向倒数第二个元素。
• left 向右移动，直到找到大于pivot的元素
• right 向左移，直到找到小于pivot的元素
• 如果 left 小于 right 提前将两个数交换。然后重复以上步骤。
• 当 left > right 时，本次分区结束。left 的位置就是 pivot 最终应该在的位置

const partition = (arr, low, high) => {
  const pivot = arr[high]

  let left = low;
  let right = high - 1;
  while (left <= right) {
    while (left <= right && arr[left] <= pivot) left++
    while (left <= right && arr[right] > pivot) right--

    if (left < right) {
      [arr[left], arr[right]] = [arr[right], arr[left]]
      left++
      right--
    }
  }
  [arr[left], arr[high]] = [arr[high], arr[left]]
  return left;
}
const quickSort = (arr, low = 0, high = arr.length - 1) => {
  if (low >= high) {
    return
  }

  const pivotIndex = partition(arr, low, high)
  quickSort(arr, low, pivotIndex - 1)
  quickSort(arr, pivotIndex + 1, high)
}

复杂度分析

• 时间复杂度：最坏时间复杂度 O(n^2), 最好时间复杂度 O(nlogn)，平均时间复杂度 O(nlogn)。
• 空间复杂度：O(1)
• 不是稳定的排序

总结

• Pivot 元素的选取很重要

资源与参考

[1] CMU algorithm complexity
[2] 凯耐基梅隆大学数据结构与算法
[3] 十大经典排序算法
[4] visualgo 排序动画演示 [5]Wikipedia: Quick Sort