插入排序 Insertion sort

原理

先看看Wikipedia的定义：

Insertion sort algorithm iterates, consuming one input element each repetition, and growing a sorted output list. Each iteration removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there. It repeats until no input elements remain.

所以插入排序的思路就是：

• 把列表分为两个部分，一部分是已经排好序，一部分待排序。（这一点和选择排序类似）
• 初始将第一个元素作为有序子列为，然后每次迭代从有序序列中移除；然后将它插入到有序序列中的相应位置。
• 重复以上步骤，直到到最后一个元素，则表示数组有序。

图示

可以通过动画演示理解, 以下网上找的两个动画。如果你想操作不同的参数来演示，可以上这个网站visualgo.net动手试试。

图示1

图示2

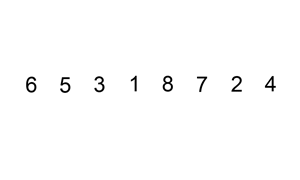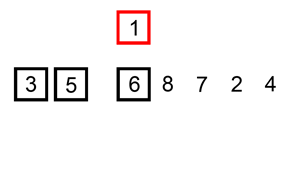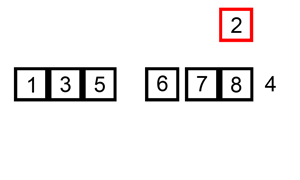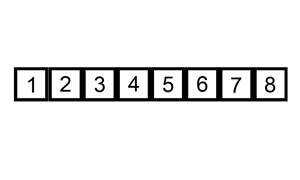
代码实现

关于代码，README中代码只有实现算法的函数，具体运行的代码，请查看该目录下的文件。

代码如下：

const insertSort = (array) => {
    // 不修改原数组
    const originValues = array.slice(); 

    // 初始将第一个元素指定为有序子列，从第2个元素开始插入，直到n-1元素 
    for (let i = 1; i < originValues.length; i++) {
        const currentValue = originValues[i];
        // 标记插入有序子列的位置
        let insertIndex = i;
        // 将当前元素从右到左与有序子列元素比较
        // 起始位置为当前元素前一个元素，即i-1,终止位置为0
        // 如果当前元素比该有序子列元素小，则该元素后移一位，并修改插入位置的游标
        for (let j = i-1; j > -1 && currentValue < originValues[j]; j--) {
           originValues[j+1] = originValues[j];
           insertIndex = j;
        }
        // 插入指定位置
        originValues[insertIndex] = currentValue;
    }

    return originValues;
};

以上就是直接插入排序的代码实现。总体来说还是比较简单易懂，其实就类似于打扑克，不断将扑克牌按顺序插入指定位置。唯一可能有一点容易想不清楚的，就是有序子列的右移部分。想清楚一点，只要有序子列的该元素大于要插入的元素，该元素就要后移一位。

算法分析

1. 时间复杂度
排序算法中，两个元素的比较次数是影响运行时间的首要因素。所以我们可以通过这个层面来评估。
最优复杂度
当数组有序时，每一次迭代只有一次比较，所以总共有n-1次比较，复杂度为O(n)。
最差复杂度
当数组逆序时，每一次都要比较整个有序子列，比较次数为:

T(n) = 1 + 2 + ... + n-1 = n*n/2

所以，最差复杂度是O(n²)。

2. 稳定性
因为比较元素是，相同值不会交换，所以插入算法是稳定的。

总结

本章节介绍了插入排序的实现。插入排序在思路上，和选择排序还是有些类似的。插入排序的复杂度还是没有突破O(n²)。
不过，上面的实现只是简单的插入排序，还可以优化。就是在有序子列中找插入位置时，利用二叉查找的方法，这样复杂度可以到O(nlogn)。这里先不做介绍。

参考

[1] 动画演示
[2] tutorials point 教程
[3] Sorting Algorithms
[4] 凯耐基梅隆大学数据结构与算法-排序算法